Assalamualaikum warahmatullah. If you ever register to the web and put a username, you might be wondering how did they know that the username was already taken or not, just in milliseconds? Ok that’s the Bloom Filter behind it.
Apart from that, Google BigTable, in its research paper mention that it also uses Bloom Filter to drastically reduces the number of disk seeks required for read operations. Also another DBs like Apache HBase, Cassandra, PostgreSQL, use Bloom Filter to reduce disk access to improve performance.
Another use cases, Medium uses Bloom Filter to avoid recommending article that has previously read by a User. Google Chrome used Bloom Filter to identify Malicious URLs, so the URLs will first checked by Bloom Filter and Chrome will give us a warning if the URLs are suspicious.
Okay, enough examples, what is Bloom Filter anyway?
According to Wikipedia: A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set.
I don’t understand every single word in that sentence
In a simple term, you can check whether an element is present on a list, using less storage & time.
And why is it called probabilistic data structure? If you take a closer look at this post’s title: “It’s Not There, or It’s Probably There!”, there’s a word probably, means that when Bloom Filter said that an element is present on a list, it’s actually not 100% sure. BUT, if Bloom Filter said that an element is not present, it can be guaranteed, one-hundred-percent, that an element is really not present on a list. In other words, Bloom Filter can have False Positive results, but not False Negative. Then, you can actually say that you use Bloom Filter to check whether an element is certainly NOT present on a list.
Is it enough to have 100% guarantee only at the negative results? At some cases, yes. Take Google BigTable implementation as the example, by using Bloom FIlter, it doesn’t need to check to the actual data (disk seek) if Bloom Filter already said that the data is not present. That way, BigTable can drastically improve the read performance.
So, how does Bloom Filter works?
The 2 important parts of the Bloom Filter are Hash Function and Bit Array. The number of hash function used is highly influence the False Positive ratio. Basically, what Bloom Filter do when we insert new element is:
- Hash the element to
knumber of hash function, resultingknumber of hash code - For every hash code generated by
kfunction, use hash code as index of Array set the Bit Array to 1
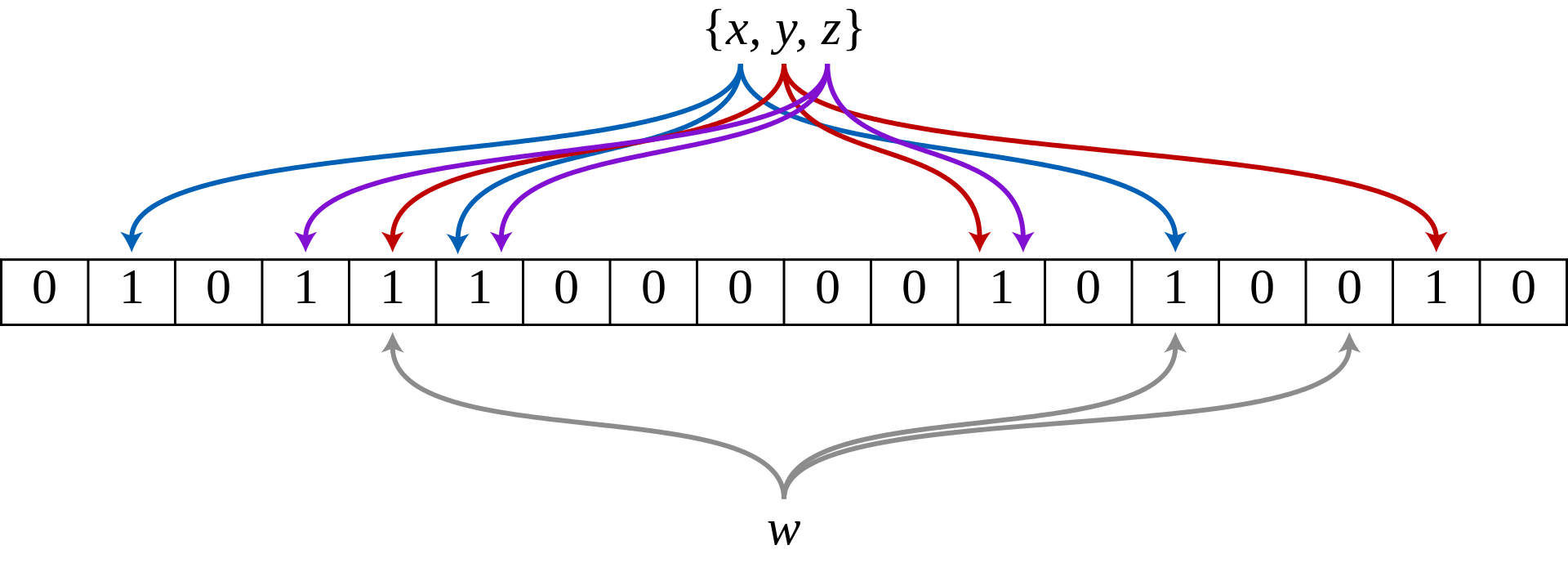
In the image above we have 3 Hash Function. We pass the string x, y and z to the Hash Functions and will generate 3 different hash code. For example x will be hashed into 1, 5, and 13, thus, we set the Bit Array with index 1, 5 and 13 to 1. Same goes with y and z.
When we want to check whether the element is present on the list, what Bloom Filter do is:
- Hash the element to
knumber of hash function, resultingknumber of hash code - Check whether all the index generated by
Hash Functionare set to1, if one of them is not set to1, we can certainly say that the element is not present.
In the example above, we check whether w is present on the list. The element w is hashed into 4, 13, and 15. Bloom filter will check whether 4, 13, and 15 index in Bit Array are set to 1. Because the index 15 is set to 0, Bloom Filter will say that w is not present on the list.
Again, there is a possibility that Bloom Filter will generate False Positive results. For example, let’s say we have another entry named q, then when we pass q into hash functions, it hashed into 1, 3, and 4. When Bloom Filter do checking, all the index for q are set to 1 so Bloom Filter say that the element is present, while in fact, it’s not.
Implementation
Warning! This implementation is for academic purposes only, not intended to be used in the real world/production environment. There have been many implementations of Bloom Filter that you can use them right away e.g Python’s bloom-filter or Google’s Guava.
First, we need to calculate Bit Array size needed by Bloom Filter, based on the item size and False Positive probability.
Note that item size is not the actual size, it’s basically the maximum number of entries to keep false positive rate as expected. If, say, we set item size 100 and false positive probability 0.1, then we put more than 100 entries, Bloom Filter doesn’t guarantee the false positive probability anymore, it might be more than 0.1.
def getNumberOfBits(n: Int, e: Double): Int = {
-((n * math.log(e)) / (math.pow(math.log(2), 2))).toInt
}
Then we need to calculate the optimal number of Hash Function.
def getNumberOfHashFunc(m: Int, n: Int): Int = {
((m / n) * math.log(2)).toInt
}
For the hash functions, in this example I use MurmurHash3, but you can also use Jenkins’ Hashes or any other hash function as long as it’s independent and uniformly distributed. I useseed to make sure that every hash function will get different hash code.
def getHash(str: String, seed: Int): Int = {
util.hashing.MurmurHash3.stringHash(str, seed)
}
To add entries to the Bloom Filter, we need to create add function. The add function will hash the entry into several hash code based on the number of hash function. The hash code then will be stored on scala’s BitSet, which basically sets of non-negative integers which are represented as variable-size arrays of bits packed into 64-bit words. We also need to do modulo for the hash code by bitSize to maintain the size of the BitSet.
def add(str: String): Unit = {
def add(str: String, seed: Int): Unit = {
if (seed == hashSize) return
val hashed = (getHash(str, seed) >>> 1) % bitSize
bitSet += hashed
add(str, seed+1)
}
add(str, 0)
}
Finally, to check whether the entry is NOT present on the list, we need to hash the element first, then check whether the element is not present on the BitSet. If yes, we can safely say that the element is not present. But if all of the hash code is present, we can say that the element is probably present.
def contains(str: String): Boolean = {
def contains(str: String, seed: Int): Boolean = {
if (seed == hashSize) return true
val hashed = (getHash(str, seed) >>> 1) % bitSize
if (!(bitSet(hashed))) return false
contains(str, seed + 1)
}
contains(str, 0)
}
To wrap them all, i create a new Class named BloomFilter with parameters itemSize to specify possible number item of the entries, and falsePositiveProb to specify the accepted False Positive Probability which will affect the number of bit and the number of hash function that we use. Some of the function & values are set to private because we don’t need to expose them. The users only need to use add and contains functions, also bitSize and hashSize values.
import scala.collection.immutable.BitSet
class BloomFilter(itemSize: Int, falsePositiveProb: Double) {
private def getNumberOfHashFunc(m: Int, n: Int): Int = {
((m / n) * math.log(2)).toInt
}
private def getNumberOfBits(n: Int, e: Double): Int = {
-((n * math.log(e)) / (math.pow(math.log(2), 2))).toInt
}
private def getHash(str: String, seed: Int): Int = {
util.hashing.MurmurHash3.stringHash(str, seed)
}
private var bitSet = BitSet()
val bitSize = getNumberOfBits(itemSize, falsePositiveProb)
val hashSize = getNumberOfHashFunc(bitSize, itemSize)
def add(str: String): Unit = {
def add(str: String, seed: Int): Unit = {
if (seed == hashSize) return
val hashed = (getHash(str, seed) >>> 1) % bitSize
bitSet += hashed
add(str, seed+1)
}
add(str, 0)
}
def contains(str: String): Boolean = {
def contains(str: String, seed: Int): Boolean = {
if (seed == hashSize) return true
val hashed = (getHash(str, seed) >>> 1) % bitSize
if (!(bitSet(hashed))) return false
contains(str, seed + 1)
}
contains(str, 0)
}
}
Let’s try to create a Bloom Filter object.
scala> val itemSize = 100
val itemSize: Int = 100
scala> val falsePositiveProb = 0.1
val falsePositiveProb: Double = 0.1
scala> val bloom_obj = new BloomFilter(itemSize, falsePositiveProb)
val bloom_obj: BloomFilter = BloomFilter@6d5f4900
scala> bloom_obj.bitSize
val res7: Int = 479
scala> bloom_obj.hashSize
val res8: Int = 2
If we check the bit size and hash size, we can see that to store 100 entries with false positive probability of 0.1, we need 479 bitSet and 2 hash functions. With 479 BitSet, we may say that to store 100 entries/information we only consumes ~64 bytes of memory. Comparing to store 100 strings, it’s much more space-efficient.
Now let’s try to put some data to the Bloom Filter with the item size of 10.
scala> val bloom_obj = new BloomFilter(10, 0.1)
val bloom_obj: BloomFilter = BloomFilter@79871528
scala> bloom_obj.add("car")
scala> bloom_obj.add("can")
scala> bloom_obj.add("cat")
scala> bloom_obj.add("man")
scala> bloom_obj.add("hen")
scala> bloom_obj.add("chicken")
Then try to check some entries
scala> bloom_obj.contains("chicken")
val res33: Boolean = true
scala> bloom_obj.contains("no entries")
val res34: Boolean = false
If we check the entry chicken, Bloom Filter will return true, and if we check no entries, Bloom Filter will return false. Works as expected. Now let’s add more entries.
scala> bloom_obj.add("house")
scala> bloom_obj.add("hospital")
scala> bloom_obj.add("airport")
scala> bloom_obj.add("station")
scala> bloom_obj.add("office")
Then we check some values again.
scala> bloom_obj.contains("mall")
val res48: Boolean = false
scala> bloom_obj.contains("no entries")
val res40: Boolean = false
scala> bloom_obj.contains("home")
val res41: Boolean = false
scala> bloom_obj.contains("m")
val res50: Boolean = true
Notice that False Positive result happen, Bloom Filter said that m entry is present, while in fact it’s not. Again, no matter how many entries we store to the Bloom Filter, space-wise it’s constant, but we sacrifice the False Positive Probability as it will getting higher.
This post, however, is not going deeper into mathematical calculation of Bloom filter. But if you’re interested, you can find it on wikipedia and Bloom Filter paper.
Wassalamualaikum warahmatullah


